
Ally Learn - Quiz on Ring Theory PRIME Ideal of a Ring - A simple and useful concept in Ring Theory Learn the concepts of Higher Mathematics from about 900 video lectures

SOLVED: Assume R is commutative ring: Prove that the intersection of two ideals in ring R is also an ideal. If I,J are ideals of a ring R, define I + J =
![PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/ad9be6262045ba725d366791d0badfcbd6010d9a/7-Figure2-1.png)
PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar

abstract algebra - Visualizing quotient polynomial rings are fields for maximal ideals which are generated by irreducible monic - Mathematics Stack Exchange

Amazon.com: iDeal Of Sweden Magnetic Ring Mount (Attachable Selfie & View Stand) (Gold) : Cell Phones & Accessories

Q)Chapter-14(ring theory) - Chapter - 14 (Ideals and Factor Rings) Dr. Sunil Kumar Yadav and Ms. - Studocu


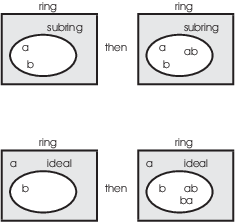

![PDF] Signature Standard Bases over Principal Ideal Rings | Semantic Scholar PDF] Signature Standard Bases over Principal Ideal Rings | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/651ba51c455156974f6cee98ca07a2ec9b01b236/146-Table3.2-1.png)










